
A B /Q
0,0 /0 0,1 /1 1,0 /1
A B / Q
1,1 /1 1,0 /0 0,1 /0
11.2 ARDIŞIL DEVRELERİN ANALİZİ
11.2.1 Tanım
Ardışıl devre, bileşiminde en az bir FF bulunduran, bunun ötesinde giriş-çıkış
durumunu belirleyen bileşik devreler (lojik kapılar) içeren düzeneklerdir.
Ardışıl devrelerin davranışı; girişlerine, çıkışlarına ve mevcut
durum ile alabilecekleri gelecek durumlara göre
belirlenir. Ardışıl bir devrenin analizi; girişlerin, çıkışların ve iş sırası
tablosu veya şemasının elde edilmesi şeklinde gerçekleştirilir. Ardışıl
devrelerin davranışını tanımlayan boolean ifadeleri yazılabilir. Ancak, bu
ifadelerin doğrudan veya dolaylı olarak gerekli zaman sırasını içermesi gerekir.
Genel özellikleri tanımlanan bir ardışıl devrenin analizi üç değişik yöntemle yapılabilir :
I- Durum Geçiş Şeması Yöntemi,
II- Durum Geçiş Tablosu Yöntemi,
III- Durum Denklemleri Yöntemi,
Bu yöntemleri sırası ile açıklayalım.
11.2.2 Durum Geçiş Şeması Yöntemi
Durum geçiş şeması yöntemi; ardışıl devrenin sözel
anlatımını en iyi yansıtan, mevcut durum-gelecek durum
ilişkisini görsel biçimde sergileyen bir yöntemdir. Bu yöntemde, devrenin her
durumu bir daireyle, durumlar arasındaki geçişler
ise daireleri birbirine bağlayan yönlü oklar ile
gösterilir. Her dairenin içindeki ikili sayı, dairenin temsil ettiği durumu
tanımlar. Geçişleri gösteren oklar üzerine ise söz
konusu durum geçişinin hangi girdilerle gerçekleştiği ve
çıktının ne olduğu yazılır. Bu gösterim için kesme işareti (/) kullanılır ve bu
kesme işaretinin soluna girdiler, sağına ise çıktılar yazılır. Bir durum
değişikliği söz konusu değil ise, durum geçiş oku başladığı noktaya döner (Şekil
11.14).
Örnek 11.2 Tam toplayıcı işlemini ardışıl devre ile gerçekleştirmede oluşan olayları inceleyelim.
Bir toplayıcı devresinde elde terimi ‘E’, giriş değişkenleri ise ‘A’ ve ‘B’ sembolleriyle gösterilebilir. Sözgelimi E=0 iken, giriş değerleri A=1, B=1 olduğunda E=1 durumuna geçer ve toplayıcının çıkışı ‘0’ olur. E=1 durumunda iken; A=0, B=0 dışındaki giriş değerlerinde devrenin durumunda bir değişiklik olmaz (Şekil 11.14).
Kesme ‘/’ işaretinin solundaki değerler ‘A’ ve ‘B’ girişlerini, sağındaki terim ise ‘Q’ çıkışının durumunu ifade eder. Giriş değerlerinin toplamı daire içerisindeki ‘E’ değerini, ‘Q’ ise devrenin alacağı konumu ve E’ nin yeni değerini belirler. Örneğin E=0 iken; girişlerin ‘0,1’ olması durumunda E=0 konumunu korurken, Q=1 değerini alır. Bu durumda geçiş oku başladığı daireye geri döner. E=1 iken; girişlere ‘0, 0’ uygulanması durumunda Q=1 değerini alırken, ‘E’ durum değiştirerek ‘0’ değerini alır. Geçiş oku E=0 olan diğer daireye doğru değişimi gösterir.
|
|
||
|
A B /Q 0,0 /0 0,1 /1 1,0 /1 |
A B / Q 1,1 /1 1,0 /0 0,1 /0 |
|
|
a) Ardışıl toplayıcı blok şeması. |
 |
|
b) Ardışıl toplayıcı durum geçiş şeması. |
Şekil 11.14 Ardışıl toplayıcı blok şeması ve durum geçiş şeması.
Örnek 11.3 Paralı satıcı kutu kola makinesi
Değişik yerlerde karşılaştığımız paralı kola satıcı makinenin durum geçiş şemasını çizelim. Makinenin girdilerinin 25, 50, 100 ve 250 birimlik madeni paralar olduğunu varsayalım. Çıkışında ise kutu kola düşsün ve gereğinde paranın üzerini versin. Kolanın 150 birim değerinde olduğunu varsayarak, makinenin alacağı durumları; boş, kasada 25 var, kasada 50 var, kasada 75 var, kasada 100 var ve kasada 125 var diye sıralayabiliriz. Bu değerleri kasanın alacağı durumlar kabul ederek daireler içerisinde gösterebiliriz.
Makine ‘kasada 125 birim var durumuna geldikten sonra hangi para atılırsa atılsın bir kola kutusu düşmekte, paranın üstü geri verilip makine boş durumuna dönmektedir. Kasada olabilecek paraları durumlar olarak tespit ettikten sonra atılabilecek para birimlerini ‘/’ işaretinin solunda gösterip, ‘/’ işaretinin sağında ise kolanın düşüp (1), düşmediği (0) ve ayrıca kalan para miktarı gösterilirse, (şekil 11.15)’deki durum şeması elde edilir.
 |
|
Şekil 11.15 Kutu kola makinası için durum geçiş şeması. |
Bu örnekte sözel anlatımla geçiş şemasını çıkardık. Lojik şeması çizilen ardışıl
devrede durum geçiş şeması da oluşturulabilir.
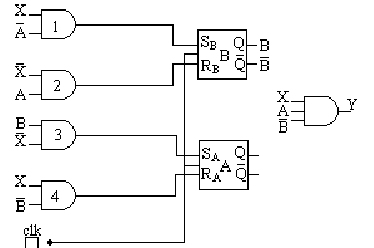
Örnek 11.4 Şekil 11.16’da verilen mantık devresi, ardışıl bir fonksiyonu gerçekleştirmektedir. Devrenin girişi ‘x’, çıkışı ‘y’ olarak; durumları da ‘A’ ve ‘B’ ifade edilidiğinde devrenin durum şemasını oluşturalım. Devrenin incelenmesine bir başlangıç durumundan (örneğin AB=00 gibi) başlanır. X=1 olduğunda, FF girişleri;
değerini alır. Bu giriş değerlerine sahip FF’lerin bir sonraki
durumu AB=01 olarak belirlenir. Bu anda devrenin çıkışı;
![]() olur.
olur.
Devrenin incelenmesinden; devrenin alabileceği durumları temsil eden AB değişkenlerinin, 00, 01, 10 ve 11 kombinasyonlarını alabileceği anlaşılır. Bu kombinasyonlar devrenin durumları olarak alınıp devredeki durum değişkenleri incelenirse, şekil 11.17 ’deki durum geçiş şeması elde edilir. Devrenin çalışmasını yorumlamaya yardımcı olan durum şemasını bu şekilde elde etmek karmaşık bir yöntemdir. Bu nedenle, bir devrenin durum şeması daha sonra anlatılacak durum tablosundan doğrudan çizilebilir.
 |
|
Şekil 11.16 Ardışıl devre lojik şeması. |
 |
|
Şekil 11.17 Ardışıl devrenin durum şemasının çizilmesi. |
11.2.3 Durum Geçiş Tabloları Yöntemi
Durum geçiş tablosu, ardışıl bir devrede mevcut durum ve
giriş-çıkış değişkenleri arasındaki ilişkileri sergileyen bir
tablodur. Bu tablo hazırlanırken, devrenin durum değişkenleri sayısı ile
girdilerin sayısı göz önüne alınır. Durum geçiş tablosunda, flip-flopların tetiklenme
palsinden önceki durumunu belirten ‘mevcut durum’, tetiklenme palsi
uygulandıktan sonraki durumu ifade eden ‘sonraki durum’ ve ‘çıkış’ olmak üzere
üç kısım bulunur. Hem sonraki durum, hem de çıkış bölümleri, X=0 ve X=1 için
olmak üzere 2 sütundan oluşur. Tabloyu oluştururken, durum değişkenleri sayısı
ile girdi sayısı göz önüne alınır. Buna göre devrede ‘m’ tane FF varsa,
‘m’ tane durum değişkeni tanımlanır ve devrede 2m tane değişik durum
söz konusu olur. Ayrıca devrenin ‘n’ tane girişi varsa, 2n tane
farklı giriş değerleri birleşimi söz konusu olur. Tablo oluşturulurken, önce değişken
bileşimlerini içeren bir sütun hazırlanır. Daha sonra, durum tablosunun
oluşturulmasına varsayılan bir ilk değerle başlanır. Analiz
her ne kadar keyfi bir durumla başlayabilirse de, şekil 11.16’da ki devreyi
incelemeye ‘00’ durumu ile başlayacağız. Mevcut durum ‘00’ iken; A=0 ve
B=0 olur. Bu anda her iki FF reset konumunda ve X=0’dır. Bu değerlerin
uygulandığı şekil 11.16’da ki, ‘VE’ kapılarından hiç
birisi lojik '1' sinyali üretmez ve
dolayısıyla sonraki durum değişmeden kalır. Bu
durumda, AB=00 ve X=0 iken, tetikleme sinyalinden sonraki durum ‘00’ olarak
belirlenir. AB=00 iken X=1 olunca; 1. kapı B FF’ sinin S girişine ‘1’ sinyali üretirken, 4.
Kapı A FF’sinin R girişine ‘1’ sinyali üretir. Tetikleme sinyali FF’leri
tetikleyince, A FF’si çıkışı ‘0’ ve B FF’si çıkışı ‘1’ olur. Bu bilgiler tabloya
taşınırsa, sonraki durum AB=01 olarak oluşur. Aynı
şekilde diğer üç olası mevcut durumdan başlayarak sonraki durumlar elde
edilebilir. Elde edilen değerler; girişlerin, mevcut durumun ve kullanılan FF
türünün bir fonksiyonudur (Tablo 11.4).
|
Tablo 11.4 Şekil 11.16’daki devrenin durum geçiş tablosu. |
|
Mevcut Durum |
Sonraki Durum |
Çıkış |
|
AB |
AB AB |
Y Y |
|
00 |
00 01 |
0 0 |
Lojik devreden çıkış bölümünün değerlerini bulmak daha kolaydır. Örnek devrede, yalnızca X=1, A=1 ve B=0 iken ‘y’ çıkışı 1’e eşittir. Bu nedenle; mevcut durum=10 ve X=1 durumunda y=1, bu durum dışındaki bütün durumlarda çıkış sütunları '0' olarak yazılır. Ardışık bir devrenin harici çıkışları , mantık elemanlarından ve FF çıkışlarından alınabilir. Mantık kapılarından çıkış alınması halinde durum tablosunda çıkış bölümü gereklidir. Çıkış olarak yalnızca FF çıkışları söz konusu ise, FF’lerin çıkışları mevcut durum sütununda zaten verildiğinden durum tablosunun çıkış bölümü iptal edilebilir.
Tablo 11.5 Ardışıl makinaya ilişkin durum tablosu
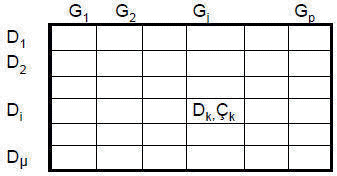
(a) Bir ardışıl makinaya ilişkin genel durum tablosu

(b) Seri toplayıcıya ilişkin durum tablosu
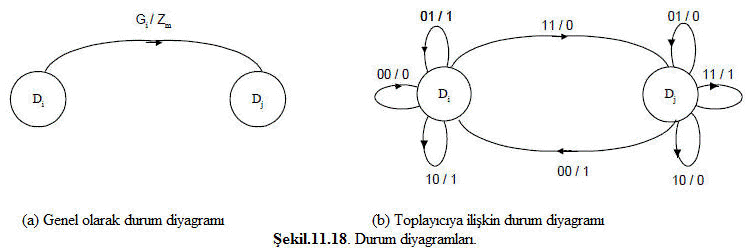
Durum diyagramı, düğümler ve topolojik elemanlardan oluşmuş bir diyagramdır. Düğümler durumlara karşı düşer. Makine Di durumunda iken Gi girişi altında DJ bir sonraki durumuna gidiyor ve çıkış zm ise, Di düğümünden DJ düğümüne yönlendirilmiş bir topolojik eleman çizilir ve üzerine Gi / zm yazılır.(Şekil 11.18 a)'da durum diyagramının bir parçası gösterilmiştir. Örnek 11.1 deki seri toplayıcı için durum diyagramı (Şekil 11.18 b) deverildiği gibidir. Girişler ve durumlar ilgili değişkenler cinsinden verilmiştir
11.2.4 Durum Denklemleri Yöntemi
Durum denklemleri, flip-flop’ların durum geçiş
şartlarını tanımlayan matematiksel bir ifadedir. Denklemin
sol tarafı FF’ nin sonraki durumunu, bir boolean fonksiyonu olan sağ taraf ise
sonraki durumu 1’e eşitleyen mevcut durum
şartlarını tanımlar. Sonraki durum şartlarının
harici giriş değişkenleri ve FF değerleriyle tanımlaması
dışında, durum denklemi şeklen FF karakteristik denklemine benzer. Durum
denklemi, doğrudan doğruya durum tablosundan elde edilir. Örneğin; A FF’sine ait
durum denklemi Tablo11.4 ’den elde edilebilir. Sonraki durum sütunlarından
A FF’ sinin ‘1’ durumuna dört kez geçtiğini
görürüz. Bu durumlar; X=0 iken AB= 01, 10, 11 durumları ile, X=1 iken AB=11
olduğu bileşenlerdir. Anlatılanlar bir durum denkleminde matematiksel olarak;
formülü ile ifade edilebilir. Denklemin sol tarafı; FF’nin harf sembolünü ve FF’nin bir sonraki alacağı değeri ifade eden zaman fonksiyon sembolünü içerir [A(t+1)]. Aynı şekilde, B FF’sinin dört kere ‘1’ değerine sahip olduğu durum tablosunda görülmektedir. Bu durumda, tablodan faydalanarak B FF’si için;
denklemi yazılabilir.
Durum denklemlerinin sağ tarafı mevcut durum için bir boolean fonksiyonudur. Bu
fonksiyon 1’e eşit olunca, bir sonraki tetikleme palsi ile A FF’sinin sonraki
durumu ‘1’ olur. Fonksiyonun ‘0’ olması ise sonraki durumu ‘0’a eşitler.
|
|
|
Şekil 11.19 FF durum denklemlerinin Karnaugh haritası yardımıyla sadeleştirilmesi |
A ve B FF’ lerinin durum denklemleri, (şekil 11.19) ’daki Karnaugh haritaları ile sadeleştirilebilir. Yukarıda bulunan durum denklemleri Karnaugh haritalarına taşınır ve Karnaugh yardımıyla sadeleştirme yapılırsa sadeleştirme sonucunda;
denklemleri bulunur.