
2.1 SAYI SİSTEMLERININ İNCELENMESİ
2.1.1 Tanım
Onluk sayı düzeni, insanların günlük hayatta kullanması için yatkın olmasına
rağmen, günümüz bilgisayar teknolojisi için uygun değildir. Bu nedenle günümüz
bilgisayar teknolojisinde değişik sayı düzenleri kullanılmaktadır. Bunlar:
• Decimal (Onlu) Sayı Sistemi
• Binary (İkili) Sayı Sistemi
• Octal (Sekizli) Sayı Sistemi
• Hexadecimal (Onaltılı) Sayı Sistemi' dir.
Sayı sistemlerini incelerken göz önünde bulundurmamız gereken ilk kavram; sayı sistemlerinde kullanılan rakam, işaret, karakter veya harfleri açıklamak ve bunların temsil ettikleri anlamları belirlemektir.
Sayı sistemlerinde kullanılan rakamın / harfin / karakterin, sayı içerisinde bulunduğu yere (basamağa) bağlı olarak temsil ettiği anlamı değişir. Anlam değişikliğini belirleyen unsur, bulunan basamağın sayı sistemine bağlı olarak taşıdığı kök / taban değeridir. Bu durumda sayı sistemine bağlı olarak değişen ikinci kavram; sayı sistemlerinde kullanılan taban değeridir.
Bir sayı sisteminde; kullanılan rakam/karakterleri ‘d’ ve sayı sistemini ‘R’ ile ifade edersek;
S = dnRn + dn-1Rn-1 +................+d2R2+d1R1 +d0R0 eşitliği elde edilir.
Her rakam, bulunduğu basamağın köke bağlı basamak değeri ile çarpılır ve temsil ettiği sayı bulunur. Bütün rakamların temsil ettiği sayılar toplanarak sonuç elde edilir.
Not: Bir sayı sisteminde kullanılan rakamlar her zaman taban değerinden küçük olmak zorundadır.
Ondalıklı sayılar için;
S = dnRn + dn-1Rn-1 +................+d2R2+d1R1 +d0R0 , d1R-1 +d2R-2 +d3R-3+ ... eşitliği kullanılır.
2.1.2
Decimal (Onlu) Sayı Sistemi
Decimal (onlu) Sayı sistemi günlük hayatta kullandığımız 0 1 2 3
4 5 6 7 8 9 rakamlarından oluşur. Decimal (onlu) Sayı sisteminde her sayı
bulunduğu basamağa göre değer alır. Sistemin tabanı 10’ dur.
Örnek 2.1 042.203.005 Sayısını analiz edelim;
5x100 = 5 0x101 = 0 0x102 = 0 3x103 = 3.000 0x104 = 0 2x105 = 200.000 2x106 = 2.000.000 4x107 = 40.000.000 0x108 = 0
Sonuç: 5x100 + 0x101 + 0x102 + 3x103 + 0x104 + 2x105 + 2x106 + 4x107 + 0x108 = 042.203.005 sayısını elde ederiz.
Örnek 2.2 2784 sayısını analiz edelim.
2784=2x103+7x102+8x101+4x100
2784=2x1000+7x100+8x10+4x1
2784=200+700+80+4
2784=2784 elde ederiz.
Örnek 2.3 568,25 Sayısını analiz edelim;
568,25=5x102+6x101+8x100+2x10-1+5x10-2
568,25=500+60+8+,2+0,05
568,25=568,25 elde ederiz.
2.1.3
Binary (İkili) Sayı Sistemi
Binary (İkili) Sayı sisteminin tabanı 2’ dir. Ve bu sistemde
sadece “0” ve “1” rakamları kullanılmaktadır. Binary (ikili) Sayı sisteminde
bulunan her ‘0’ veya ‘1’ rakamları BIT (Binary Digit) adı ile tanımlanır.
Decimal (onlu) sayıları, sadece iki rakamdan oluşan Binary (ikili) sayılarla
tanımlayabilmemiz, sayısal sistemlerin iki voltaj seviyesini kullanarak farklı
büyüklüklerin tanımlanmasının anlaşılmasını sağlamaktadır.
İkili sayı sistemini kullanmamızın nedenleri aşağıda maddeler halinde sıralanmıştır.
a) Boole cebrine dayanan lojik verilerin temsili ve lojik işlemlerin gerçekleştirilmesi için en uygun olan sayı sistemidir.
b) Aritmetik işlemlerin basit ve hızlı bir şekilde gerçekleştirilmesini sağlar.
c) Çoğu fiziki olaylar ikili sistem için çok müsaittir. Mesela gerilim var/yok, ışık var/yok, kontak açık/kapalı, magnetlenme var/yok vs.
d) Bilgisayarlarda veri ile ilgili bellekteki adresi belirtmek için kullanılır.
e) Komut kodu olarak kullanılır.
f) Alfabetik ve sayısal olmayan karakterleri temsil etmek için kullanılır.
g) Bilgisayarlarda dahili ve harici olarak bulunan devrelerin durumlarını belirlemek için bir sayı grubu olarak kullanılır.
İkili sayı sisteminin bazı dezavantajları da şöyledir:
a) İnsanlar ikili sayı sistemini kullanmaya pek alışık değillerdir.
b) Onlu sayı sistemine göre çok uzun rakamlar yazmak gerekir.
Örnek 2.4 Onlu tabanda verilen 25 sayısının ikili tabandaki karşılığını bulalım. (2510 = X2);
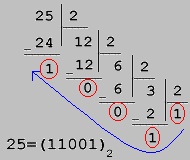
|
25 = 2 4+2 3+2 2+ 2 1+ 2 0
|
|
25 = (11001)2
|
| Sonuç X = (11001)2 elde edilir. |
Örnek 2.5 Onlu tabanda verilen 23 sayısının ikili tabandaki karşılığını bulalım. (2310 = X2);
|
23 = 2 4+ 2 3+2 2+ 2 1+ 2 0
|
|
23 = (10111)2
|
| Sonuç X2 = (10111)2 elde edilir. |
Örnek 2.6 Onlu tabanda verilen 8,875 sayısının ikili tabandaki karşılığını bulalım. (8,87510 = X2);
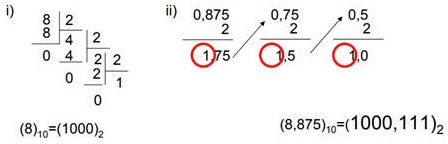
2.1.4
Oktal (Sekizli) Sayı Sistemi
Sayısal Sistemler her ne kadar ikili sayı sistemini kullansalar
da bir tasarımcı için binary (ikili) sayılarla işlem yapmak zahmetli bir işlem
olduğundan farklı sayı sistemlerinin kullanımı tasarımcılar arasında
yaygınlaşmıştır. Kullanılan bu sayı sistemlerinden Sekizli (oktal) Sayı
sisteminin tabanı sekiz olup 0, 1, 2, 3, 4, 5, 6, 7 rakamları bu sayı sisteminde
kullanılır.
İşlemci yalnız ikili sistemi anladığı, kullanıcı ise 10' lu sisteme alıştığı için 60' lı yıllara kadar bilgisayarla kullanıcı arasında iletişim zorluğu vardı. Bu zorluklar özellikle bilgisayara adres bilgisi aktarmak, bilgisayardan adres bilgisi almak, registerlerin durumlarını izleyerek gereken ayarlamaları yapmak, belleğin içeriğini kontrol etmek ve gereken değişiklikleri yapmak, işlemciye hemen kullanılacak veriyi aktarmak vs. gibi problemlerin çözümü sırasında yoğun olarak karşıya çıkmaktaydı. Bu problemi hafifletmek amacı ile 2’ li sistemden daha anlaşılır, bilgisayar için ise ikili sistem kadar anlaşılabilen bir aralık sayı sisteminin olması gerekirdi. Böyle bir sistem olarak 8’ li sayı sistemi seçilmişti. Bu tercih sebebi ise 8 = 23 olduğu için, 8' li sayının her bir rakamının yerine mekanik olarak onun 3 rakamlı ikili karşılığını koymakla 8’ li sayının 2’ li karşılığını almasıdır.
Örnek 2.7 (34507,0216)8 = (?)2
(34507,0216)8 = 011 100 101
000 111 , 000 010 001
110 sonucu elde edilir.
3 4
5 0
7 , 0 2
1 6
Örnek 2.8 Sekizlik tabanda verilen 736,4 sayısının onlu tabanda karşılığını bulalım.
(736,4)8 = (7x82 + 3x81 + 6x80 + 4x8-1) = (478,5)10 sayısı elde edilir.
2.1.5
Hexadecimal (Onaltılı) Sayı Sistemi
1960‘ larda
Latin alfabesinin ve noktalama, kontrol, matematik vs. işaretlerin genel amaçlı
bilgisayarların alfabesine girmesiyle; bilgi ölçme ve temsil birimi olarak byte
(8 basamaklı ikili kod) kabul edilmiştir. Bundan sonra 8 / 3 = 2,66 tamsayı
olmadığı için 8' li sayıların bellekte yerleştirilmesi ve incelenmesi zorlaşmış,
buna karşılık olarak iki rakamı tam bir byte' da yerleşen 16’ lı sistem
alternatifsiz bir aralık sistem olarak kullanılmaya başlamıştır. Bundan başka,
10’ lu (BCD) sayıların da her bir rakamının temsil edilebilmesi için 4 bit
gerekir. Böylece 16’ lı ve 10’ lu sayıların bellekte yerleştirilmesi yöntemi ve
araçları, bunlar üzerinde yapılan birçok işlemler ve bunları gerçekleştiren
program ve donanım araçları, büyük bir ölçüde her iki sayı sistemi için de ortak
olur. 16 = 24 olduğu için 16’ lı ve ikili sistemler birbirine direkt
olarak çevrilebilir.
16 = 24 olduğu için 16’ lı sayının her bir rakamının yerine onun 4 rakamlı 2’ li karşılığını koymakla 16’ lı sayının 2’ li karşılığını bulabiliriz.
Örnek 2.9 (A10C,B72F)16
= (?)2
1010 0001 0000 1100
, 1011 0111 0010
1111
A10C,B72F =
A 1
0 C ,
B 7
2 F
Örnek 2.10 Onaltılık F3 sayısının onlu tabanda karşılığını bulalım.
(F3)16 = [Fx(16)1+3x(160)] = (243)10 sayısı elde edilir.
Aşağıdaki tablo 0–15 arası decimal (onlu) sayıların hexadecimal karşılıklarını vermektedir.
|
Tablo 2.1 0 - 15 Arasındaki Sayıların Onlu, İkili, Sekizli ve Onaltılı Tabanda Karşılığı |
|
10' lu
|
2' li
|
8' li
|
16' lı
|
|
0
|
0
|
0
|
0
|
|
1
|
1
|
1
|
1
|
|
2
|
10
|
2
|
2
|
|
3
|
11
|
3
|
3
|
|
4
|
100
|
4
|
4
|
|
5
|
101
|
5
|
5
|
|
6
|
110
|
6
|
6
|
|
7
|
111
|
7
|
7
|
|
8
|
1000
|
10
|
8
|
|
9
|
1001
|
11
|
9
|
|
10
|
1010
|
12
|
A
|
|
11
|
1011
|
13
|
B
|
|
12
|
1100
|
14
|
C
|
|
13
|
1101
|
15
|
D
|
|
14
|
1110
|
16
|
E
|
|
15
|
1111
|
17
|
F
|