
| 2.3 SAYI SİSTEMLERİNDE DÖRT İŞLEM |
2.3.1
Tanım
Tüm sayı sistemlerinde sayılarda işaret
kullanılabilir. Yani pozitif ve negatif sayılarla hesaplama yapılabilir. Bu
gerçek göz önünde bulundurularak, onluk sayılarda hesaplama yaparken aşağıdaki
ilişkiler kullanılabilir. Bu ilişkiler bütün sayı sistemleri için geçerlidir.
a) +a + (+b) = a + b b) +a + (-b) = a - b
c) +a - (+b) = a - b d) +a - (-b) = a + b
2.3.2 Binary Sayılarda Dört İşlem
2.3.2.1 Binary sayılarda toplama
Binary (İkili) sayı sistemindeki temel toplama kuralları;
|
Tablo 2.15 Binary Sayılarda Toplama |
|
İşlem |
Cary (Elde) |
Sonuç |
|
0+0 = 0 |
Elde 0 |
Toplam 0 |
|
0+1 = 1 |
Elde 0 |
Toplam 1 |
|
1+0 = 1 |
Elde 0 |
Toplam 1 |
|
1+1 = 10 |
Elde 1 |
Toplam 0 |
|
1+1+1 = 11 |
Elde 1 |
Toplam 1 |
Binary sayı sisteminde iki sayı toplandığında eğer sonuç bir haneye sığmıyorsa bir elde (carry) oluşur.
Örnek 2.71 Aşağıda Binary (ikili) olarak verilen sayıları toplayınız.
(1110)2 (0110)2 +________ (10100)2 |
(1101)2 (1111)2 (1011)2 +________ (100111)2 |
(111011)2
(011011)2
(110101)2
(010010)2
+________
(10011101)2
|
2.3.2.2 Binary sayılarda çıkarma
2.3.2.2.1 Binary (İkili) sayı sistemindeki temel çıkarma kuralları;
Tablo 2.16 Binary Sayılarda Çıkarma
|
İşlem |
Borç |
Sonuç |
|
0-0 = 0 |
Borç 0 |
Sonuç 0 |
|
0-1 = 1 |
Borç 1 |
Sonuç 1 |
|
1-0 = 1 |
Borç 0 |
Sonuç 1 |
|
1-1 = 0 |
Borç 0 |
Sonuç 0 |
Binary sayı sisteminde de küçük değerlikli bir basamaktan büyük değerlikli bir basamak çıkarıldığında, bir üstteki basamaktan bir borç (borrow) alınır ve çıkarma işlemi tamamlanır.
Örnek 2.72 Aşağıda verilen iki binary (ikili) sayıyı çıkarınız.
(011)2
(001)2
-________
(010)2
|
Örnek 2.73 Aşağıda verilen iki binary (ikili) sayıyı çıkarınız.
2.3.2.2.2 Tamamlayıcı (Complementer) Yoluyla Çıkartma İşlemi
2 tür tamamlayıcı vardır. Bunlar;
- 1 tamamlayıcısı
- 2 tamamlayıcısı
Not :
a) (XXXX) binary sayısının 1 tamamlayıcısı (1111) binary sayısından çıkarılarak
elde edilir.
b) Pratik olarak bir binary sayının 1 tamamlayıcısı dijitlerinin tersi alınarak
bulunur. (0-1; 1-0)
c) Sayının 2 tamamlayıcısı = Sayının 1 tamamlayıcısı + 1’dir.
1 Tamamlayıcısı Yardımıyla Çıkartma :
• İlk önce
çıkan binary sayının 1 tamamlayıcısı alınır.
• İkincil olarak ana sayı ile çıkan sayının tamamlayıcısı toplanır.
• Eğer işlem sonucunda artan 1 var ise sonuç pozitif olup, gerçek sonuç için
toplam değerine 1 eklenir.
• Eğer işlem sonucunda artan 1 yok ise sonuç negatif olup, gerçek sonuç eldeki
değerin 1 tamamlayıcısıdır.

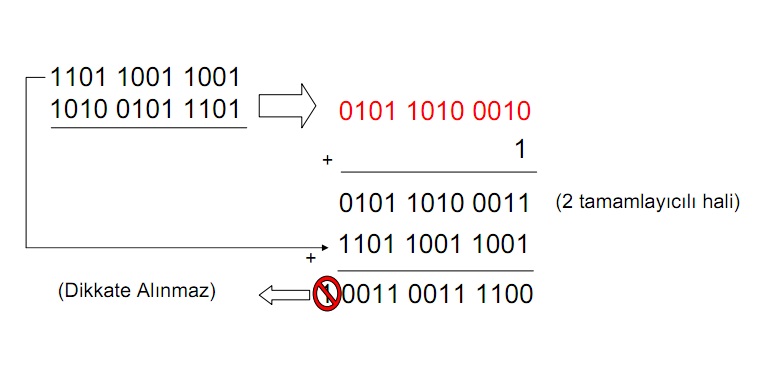
2 Tamamlayıcısı Yardımıyla Çıkartma :
• İlk önce çıkan binary sayının 2
tamamlayıcısı alınır.
• İkinci aşamada ana sayı ile çıkan sayının tamamlayıcısı toplanır.
• İşlem sonucu artan “1” olursa bu “1” sonucun pozitif olduğunu gösterir ve
dikkate alınmaz.
• İşlem sonucunda artan “1” yoksa sonuç negatif demektir. Gerçek sonuç elde
edilen sayının 2 tamamlayıcısı alınarak bulunur.
2.3.2.3 Binary sayılarda çarpma
Binary (İkili) Sayılarla Çarpma işlemi Decimal (onlu) sayı
sisteminin aynısı olup temel çarpma kuralları aşağıdaki gibidir;
Tablo 2.17 Binary Sayılarda Çarpma
|
İşlem |
Sonuç |
|
0x0 |
0 |
|
0x1 |
0 |
|
1x0 |
0 |
|
1x1 |
1 |
Örnek 2.74 Aşağıdaki iki Binary (ikili) sayının çarpımını hesaplayınız.
1011 101 x_____ 1011 0000 1011 +________ 11011110111 110 x_____ 00000 10111 10111 +_________ 10001010
Örnek 2.75 Aşağıdaki iki binary (ikili) sayının çarpımını hesaplayınız.
2.3.2.4 Binary
sayılarda bölme
Binary (İkili) Sayılarda kullanılan temel bölme kuralları
aşağıdaki gibidir. Binary (ikili) sayılardaki bölme işlemi, decimal (onlu) sayı
sisteminin aynısıdır.
Tablo 2.18 Binary Sayılarda Bölme
|
İşlem |
Sonuç |
|
0÷0 |
0 |
|
0÷1 |
0 |
|
1÷0 |
0 |
|
1÷1 |
1 |
Örnek 2.76 (1111101)2 ÷ (101)2 = ( ? )2
1111101
101
-_____
0101
101
-____
0101
101
-____
00011001
Sonuç (11001)2 olarak bulunur.
Örnek 2.77 (110)2 ÷ (10)2 = (?)2
Örnek 2.78 (1101)2 ÷ (11)2 = (?)2
2.3.3 Oktal Sayılarda Dört İşlem
2.3.3.1 Oktal
sayılarda toplama
Decimal sayı sistemindeki bütün toplama kuralları oktal sayı
sisteminde de geçerlidir.
Örnek 2.79 Aşağıda verilen toplama işlemlerini gerçekleştiriniz.
(263)8
(157)8
+_______
(442)8
|
||||
|
işlemin yapılışı |
1.Haneler |
3+7 = 2 Elde 1 | ||
|
2.Haneler |
Elde1 + 6 +5 = 4 Elde 1 | |||
|
3.Haneler |
Elde1 + 2 + 1= 4 |
Bu aritmetik işlemi, sekizli tabanda verilen sayıyı, bilinen bir sayı sistemine dönüştürerek gerçekleştirebiliriz. Aşağıda oktal sayının binary karşılıkları yazılarak aritmetik işlem gerçekleştirilmiştir
(2 6 3)8 ( 1 5 7)8 010 110 011 001 101 111 |
(010110011)2 (001101111)2
+_____________ (100100010)2
|
| Sonuç |
(100 100 010)2 ( 4 4 2 )8 |
Örnek 2.80 Aşağıda verilen toplama işlemini gerçekleştiriniz.
2.3.3.2 Oktal
(Sekizli) sayılarda çıkarma
Decimal sayı sistemindeki bütün çıkarma kuralları oktal sayı
sisteminde geçerlidir.
Örnek 2.81 Aşağıda verilen çıkarma işlemini gerçekleştirin.
(514)8
(452)8
-_______
(042)8
|
||||
|
işlemin yapılışı |
1.Haneler |
4-2 = 2 | ||
|
2.Haneler |
(Borç8+1) - 5 = 4 | |||
|
3.Haneler |
Kalan4-4 = 0 |
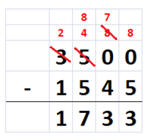
Örnek 2.82 Aşağıda verilen çıkarma işlemini gerçekleştirin.
(3500)8
(1545)8
-_______
(1733)8
|
 |
||
|
işlemin yapılışı |
|||
2.3.3.2.1 Tamamlayıcı Yardımıyla Çıkartma
7 ve 8 tamamlayıcısı olmak üzere iki adet tamamlayıcısı
vardır. 7 tamamlayıcısı binary sistemdeki 1 tamamlayıcısına; 8 tamamlayıcısı ise
2 tamamlayıcısına benzer.
• 7 tamamlayıcısı bulunurken her dijitin 7 sayısından çıkarılması gerekir.
• 8 tamamlayıcısı = 7 tamamlayıcısı +1
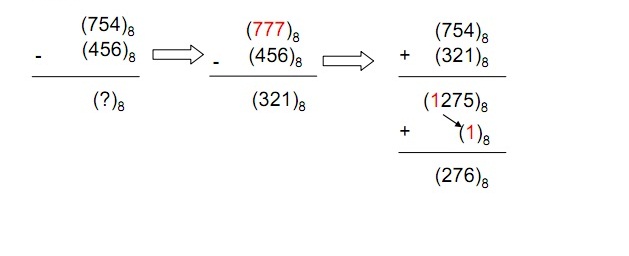
7 tamamlayıcısı ile Çıkartma :
• İlk olarak oktal sayının 7 tamamlayıcısı bulunur.
• Ana sayı ile çıkan sayının 7 tamamlayıcısı toplanır.
• Eğer belirli basamak sayısını taşan “1” varsa sonuç pozitif olup, bu “1”
sağdakilerle toplanılarak gerçek sonuç bulunur.
• Taşan “1” yoksa sonuç negatif olup, gerçek sonuç sayının 7 tamamlayıcısıdır.
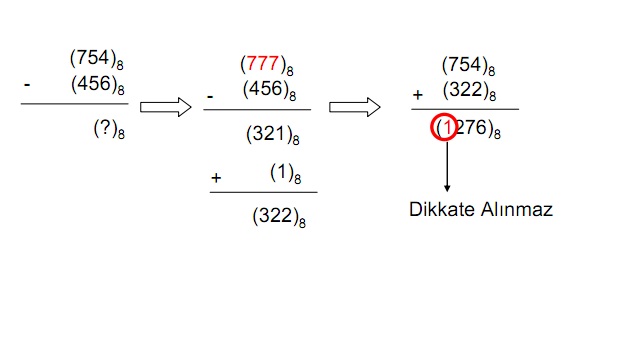
8 tamamlayıcısı ile Çıkartma :
• Çıkan sayının 8 tamamlayıcısı bulunduktan sonra bu sayı
ana sayı ile toplanır.
• Eğer belirli basamak sayısını taşan “1” var ise toplam sonucu pozitiftir ve bu
“1” dikkate alınmaz
• Taşan “1” yok ise sonuç negatiftir ve gerçek sonuç sayının 8 tamamlayıcısıdır.
2.3.3.3 Oktal sayılarda
çarpma
Decimal sayılar arasındaki sayılar arasında çarpma işlemi yapılırken,
ya decimal sayılara dönüşüm yapıldıktan sonra çarpım yapılır ve sonuç istenilen
sayı sistemine çevrilir ya da doğrudan çarpım yapılır.
Örnek 2.83 Aşağıda verilen çarpma işlemini gerçekleştiriniz.
|
|
|
(5 |
6)8 |
|
İlk işlem 6 ile 7 çarpılır. Decimal olarak 42 sayısı octal olarak (52) yazılır. 2.işlem 5 ile 7 çarpılır. Decimal olarak 35 sayısı octal olarak (43) yazılır. 3.işlem 6x2=12 sayısı octal sayı sisteminde 14 olarak yazılır. 3’ün altına 4, 4’ün altına 1 gelecek şekilde yazılır. 4.işlem olarak 5x2=10 sayısı octal olarak 12, 1’in altına 2 gelecek şekilde yazılır. Yazılan sayılar octal olarak toplanır. |
|
|
|
(2 |
7)8 |
|
|
|
|
x |
____ |
|
||
|
|
|
5 |
2 |
|
|
|
|
|
43 |
|
|
|
|
|
|
14 |
|
|
|
|
|
1 |
2 |
|
|
|
|
|
+_____ |
|
|||
|
|
2 |
04 |
2 |
|
|
Örnek 2.84 Aşağıda verilen çarpma işlemini gerçekleştiriniz.
2.3.3.4 Oktal sayılarda
bölme
Bölme işlemi decimal sayılarda olduğu gibidir. Dikkat
edilmesi gereken, çıkarma işlemini yaparken oktal sayılarda çıkarma işleminin
olduğu unutulmamalıdır.
Örnek 2.85 Aşağıda verilen bölme işlemlerini gerçekleştiriniz.
|
|
(428) 8 |
(13) 8 |
|
|
(360) 8 |
(30) 8 |
|
|
390 |
(32) 8 |
|
|
30 |
(12) 8 |
|
|
-_____ |
|
|
-____ |
|
|
|
|
032 |
|
|
60 |
|
|
|
|
26 |
|
|
60 |
|
|
|
|
-_____ |
|
|
-____ |
|
|
|
|
4 |
|
|
00 |
|
2.3.4 Hexadecimal Sayılarda Dört İşlem
2.3.4.1 Hexadecimal
sayılarda toplama
Hexadecimal sayılarla iki şekilde toplama işlemini
gerçekleştirebiliriz. Birinci yöntem sayının direk toplanması, diğer bir yöntem
ise Hexadecimal sayının herhangi bir sayı sistemine dönüştürülmeden toplama
işleminin gerçekleştirilmesi. Aşağıdaki örnekte her iki şekilde
gösterilmektedir.
Örnek 2.86 Aşağıda verilen toplama işlemlerini gerçekleştirin.
|
|
( A 1 7 )16 | |||
| ( 1 F 3 )16 |
işlemin yapılışı |
1.Haneler |
3+7 = 10(A) | |
|
+_________ ( C 0 A )16 |
2.Haneler |
1+F = 0 Elde1 | ||
|
3.Haneler |
Elde1+A+1 = C |
Örnek 2.87 Aşağıdaki iki Hexadecimal sayıyı ikili sayılara çevirerek toplayın.
(56B)16 + (47A)16 = ?
Sonuç (56B)16 + (47A)16 = (9E5)16 olarak bulunur.
Örnek 2.88 Aşağıda verilen toplama işlemini gerçekleştirin.
(A13)16
(264)16
+______
(C77) 16
2.3.4.2 Hexadecimal
sayılarda çıkarma
Hexadecimal sayılarda çıkartma işlemleri yapılırken; çıkarma
işlemini onaltılı tabanda direkt olarak yapabiliriz.
Örnek 2.89 Aşağıda verilen çıkarma işlemini gerçekleştirin.
(56B)16 – (47A)16= (0F1)16
Tamamlayıcı yolu ile çıkartma işlemi :
• 15 ve 16 tamamlayıcısı olmak üzere iki
adet tamamlayıcı vardır. 15 tamamlayıcısı binary de ki 1 tamamlayıcısına ve oktal da ki
7 tamamlayıcısına benzer.
• 16 tamamlayıcısı binary de ki 2 tamamlayıcısına ve oktal da ki 8 tamamlayıcısına
benzer.
• Sayının 1 tamamlayıcısı sayının F’den çıkarılmasıyla elde edilir.
Örnek 2.90 Aşağıda verilen çıkarma işlemini gerçekleştirin.
(F9A40)16 – (AF020)16= (4AA20)16
2.3.4.3 Hexadecimal sayılarda çarpma
Hexadecimal sayılarla çarpma işlemini direkt olarak onaltılı
tabanda yapabiliriz.
Örnek 2.91 Aşağıda verilen çarpma işlemini gerçekleştirin.
( 1 A C )16
( 2 B )16
x
-------------------
1 2 0 C
3 4 8
+
-------------------
4 6 8 C
Örnek 2.92 Aşağıda verilen çarpma işlemini gerçekleştirin.
|
(13)16 |
|
(15)16 |
|
x_____ |
|
0F |
|
05 |
|
13 |
|
+______ |
|
(18F)16 |
2.3.4.4 Hexadecimal sayılarda bölme
Hexadecimal sayılarla bölme işlemi ya direkt olarak hexadecimal (onaltılı)
tabanda yada decimal (onlu) tabana çevrim yaparak gerçekleştirilebilir.
Örnek 2.93 Aşağıda verilen bölme işlemini gerçekleştirin.
|
|
(FD2C56) 16 |
(5D) 16 |
|
|
|
BA |
(2B8E8) 16 |
|
|
|
-_____ |
|
|
|
|
432 |
|
|
|
|
3FF |
|
|
|
|
-_____ |
|
|
|
|
033C |
|
|
|
|
2E8 |
|
|
|
|
-_____ |
|
|
|
|
0545 |
|
|
|
|
516 |
|
|
|
|
-_____ |
|
|
|
|
02F6 |
|
|
|
|
2E8 |
|
|
|
|
-_____ |
|
|
|
|
E |
|
|
Örnek 2.94 Aşağıda verilen bölme işlemini gerçekleştirin.
(18F) 16 : (15) 16 = (…?…)16
(18F) 16 = 1x162+8x161+Fx160
(18F) 16 = 256+128+15
(18F) 16 = (399) 10
(15) 16 = 1x161+5x160
(15) 16 = 16+5
(15) 16 = 21
|
|
399 |
21 |
|
|
19 |
16 |
|
|
399 |
19 |
|
|
16 |
1 |
|
|
-___ |
|
|
-____ |
|
|
|
|
0 |
|
|
3 |
|
(18F) 16 : (15) 16 = (13)16
Tablo 2.19 Hexadecimal Sayılarda Toplama
|
+
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
A
|
B
|
C
|
D
|
E
|
F
|
|
0
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
A
|
B
|
C
|
D
|
E
|
F
|
|
1
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
A
|
B
|
C
|
D
|
E
|
F
|
10
|
|
2
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
A
|
B
|
C
|
D
|
E
|
F
|
10
|
11
|
|
3
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
A
|
B
|
C
|
D
|
E
|
F
|
10
|
11
|
12
|
|
4
|
4
|
5
|
6
|
7
|
8
|
9
|
A
|
B
|
C
|
D
|
E
|
F
|
10
|
11
|
12
|
13
|
|
5
|
5
|
6
|
7
|
8
|
9
|
A
|
B
|
C
|
D
|
E
|
F
|
10
|
11
|
12
|
13
|
14
|
|
6
|
6
|
7
|
8
|
9
|
A
|
B
|
C
|
D
|
E
|
F
|
10
|
11
|
12
|
13
|
14
|
15
|
|
7
|
7
|
8
|
9
|
A
|
B
|
C
|
D
|
E
|
F
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
|
8
|
8
|
9
|
A
|
B
|
C
|
D
|
E
|
F
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
|
9
|
9
|
A
|
B
|
C
|
D
|
E
|
F
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
|
A
|
A
|
B
|
C
|
D
|
E
|
F
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
|
B
|
B
|
C
|
D
|
E
|
F
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
1A
|
|
C
|
C
|
D
|
E
|
F
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
1A
|
1B
|
|
D
|
D
|
E
|
F
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
1A
|
1B
|
1C
|
|
E
|
E
|
F
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
1A
|
1B
|
1C
|
1D
|
|
F
|
F
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
1A
|
1B
|
1C
|
1D
|
1E
|