2.5 SABİT VE KAYAN NOKTALI SAYILAR

2.5.1 Sabit Noktalı Sayılar (Fixed Point Number)
Sabit noktalı sayılar, sayının tam kısmı ve ondalık kısmı ile yazılır. Bu sayı formatında tasarlanacak sisteme göre, istenilen sayının maksimum büyüklüğü ve hassasiyeti göz önünde bulundurularak sayının uzunlukları belirlenir.

Verilen sayıyı sabit noktalı sayı formatına

 sayı = i . f

formülüyle çeviririz. Burada;  i: Tam kısım (integer), f: Ondalık kısmı temsil etmektedir.

n bitlik sabit noktalı sayının matematiksel ifadesi aşağıda verilmiştir.

Sayı = x * 2^-m

Burada;
x  : aradaki virgül dikkate alınmaksızın sayının tamamını 'decimal (onlu) sayı' şeklinde ifade eder.
m : ondalık kısım (virgülden sonraki) bit sayısını ifade eder. Aşağıdaki örnekle konuyu daha iyi kavramaya çalışalım.

Örnek 2.119 3,375 sayısını sabit noktalı sayı sistemine göre inceleyiniz.

3,375 olan sayımızı 011.011 biçiminde sabit noktalı sayı formatına çevirdik. Şimdi x ve m değerlerini bulabiliriz.

x : 011.011 sayısının (aradaki virgül göz ardı edilerek) decimal sayı sistemine çevrilmesiyle bulunur.
m: 011.011 sayısının sadece ondalık kısmının decimal sayı sistemine çevrilmesiyle bulunur.

Böylece  x = 011011 = 27,
              m = 011 = 3   olarak bulunur.

Matematiksel ifadede değerleri yerine koyarsak;

Sayı = x * 2^-m formülünden;

Sayı = 27 x 2^-3
Sayı = 27 / 8
Sayı = 3,375      şeklinde ifade edilir.

2.5.1.1 Sabit noktalı sayılar formatı (fixed point number format)
Bir ikili tam sayı pozitif olduğunda işareti 0; negatif olduğunda ise işareti 1 ile gösterilir. Pozitif sayılar sadece normal ikili, negatif sayılar ise;

a) İşaretli normal ikili

b) İşaretli 1’e göre tümleyen

c) İşaretli 2’ye göre tümleyen olarak gösterilir.

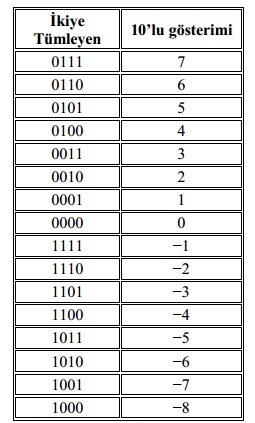
Negatif sayıların işaretli normal gösterimi bir eksi işareti ve sayının büyüklüğünden oluşur. Örneğin 8 bit kaydedicide 14 depolanmak istendiğinde +14 en soldaki işaret biti 0 olacak şekilde 00001110 şeklinde bulunur. 8. bitin sayının büyüklüğü üzerine hiçbir etkisi yoktur. Sadece işareti gösterir. -14 sayısı 8 bitte 3 farklı şekilde gösterilebilir:

İşaretli normal ikili              1  0001110

İşaretli 1’e göre tümleyen   1  1110001

İşaretli 2’ye göre tümleyen 1  1110010 sayısı ile gösterilir.

İşaretli gösterimde -14 değeri, +14 değerinin sadece işaretinin tümleyeni alınarak elde edilir. -14 sayısının işaretli 1’e göre tümleyeninde, işaret dahil tüm bitlerin 1’e göre tümleyeni alınarak veya işaretli 2’ye göre tümleyeninde, işaret dahil tüm bitlerin 2’ye göre tümleyeni alınarak +14 sayısı elde edilir.

Örneğin 0101 +5, 1101 sayısı -5 değerini göstermek için kullanılabilir. Bu gösterim metodunda ilk bit işaret biti için kullanılmaktadır.İkiye tümleyen metodunda negatif gösterilecek sayının ikiye tümleyeni alınır. Aşağıdaki tabloda bazı sayıların ikiye tümleyen metodu ile gösterimi bulunmaktadır.

Tam sayılar bilgisayarda işaretli ve işaretsiz olmak üzere iki şekilde sunulurlar (Bilgisayar, sayıların işaretli ya da işaretsiz olduğunu kullandığımız komuttan anlar.(örn. mul, imul).

Aşağıda bir sayının, tam kısmı için 5 bit ve ondalık kısmı için 7 bit kabul edilerek sabit noktalı sayı formatına dönüşümü verilmiştir.

Örnek 2.120 3,1875 sayısının sabit noktalı sayı formatına dönüştürülmesini inceleyiniz.

Sayı = 3,1875
Tam kısım = 3
Ondalık = 0,1875

Tam kısmı 5 bitlik ikili sayı şeklinde yazarsak

Tam = 00011

Ondalık kısmın çevriminde ondalık kısım, bu kısmın istendiği bit uzunluğu kadar 2 ile çarpılır. Çarpımın sonucu 1 den küçükse bit değerine 0, 1’den büyük ve eşitse bit değerine 1 yazılır ve çarpım sonucu 1’den çıkarılır. Sayı örneğimizin ondalık kısmının çevrimi aşağıda verilmiştir.

Dönüşümler sonucunda 3,1875 sayısının sabit noktalı sayı gösterimi aşağıdaki gibidir.

Yukarıda bir sayının sabit noktalı sayı formatına çevrimini gösterdik. Sabit noktalı sayının çevrimi ise yukarıda yapılan işlemlerin tam tersi şeklindedir. Aşağıda sabit noktalı sayı formatının virgüllü sayı formatına dönüşümü verilmiştir.

 Örnek 2.121 00011.0011000 sabit noktalı sayısının virgüllü sayı formatına dönüştürülmesini inceleyiniz.

Sayı = 00011.0011000
Tam = 00011
Ondalık = 0011000

Tam kısmı onluk sayı formatına aşağıdaki gibi dönüştürülür.

Tam = 0 x 2⁴ + 0 x 2³ + 0 x 2² + 1 x2¹ + 1x 2⁰
Tam = 0 + 0 + 0 + 2 + 1
Tam = 3

Ondalık kısmın dönüşümü de aşağıdaki gibidir.

Ondalık =  0 x2^-1 + 0x2^-2 + 1 x 2^-3 + 1 x 2^-4 + 0 x2^-5 + 0x2^-6 + 0x2^-7
Ondalık = 0 + 0 + 0,125 + 0,0625 + 0 + 0 + 0
Ondalık = 0,1875

Sayımızı tekrar elde etmek için tam kısım ile ondalık kısmı toplayarak sayımızı elde ederiz.

Sayı = Tam + ondalık
Sayı = 3 + 0,1875
Sayı = 3,1875

Bir sayının pozitif veya negatif olduğuna; en anlamlı bitine bakılarak karar verilir. Bu bit 0 ise sayı pozitif, 1 ise sayı negatiftir. Pozitif sayıların gösterimi yukarıda tanımlanmıştır. Negatif sayıların gösterimini ise normal ikili, bire tümleyen ve ikiye tümleyen şeklinde 3 grupta toplayabiliriz. Yukarıda elde ettiğimiz sayının negatife çevrimi aşağıdaki gibi yapılır.

 Sayı = 00011.0011000

Sabit noktalı sayı formatı ile ilgili dönüşüm işlemleri yukarıda verildi. Bu sayı formatında aritmetik işlemler aşağıda tanımlanmıştır.

2.5.1.2 Toplama ve çıkarma işlemi
Sabit noktalı sayı formatında toplama ve çıkarma işlemi ikili olarak yapılmaktadır. Aşağıda sabit noktalı sayı formatında toplama ve çıkarma işlemleri tanımlanmıştır. Bu işlemlerde tam kısım 5 bit ve ondalık kısım 7 bit alınarak yapılmaktadır.

Örnek 2.122 5,375 ve 3,1875 sayılarının sabit noktalı sayılar formatına göre toplanmasını ve çıkarılmasını inceleyiniz.

Sayı_1 = 5.375           →        00101.0110000
Sayı_2 = 3.1875         →        00011.0011000

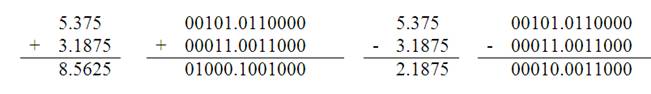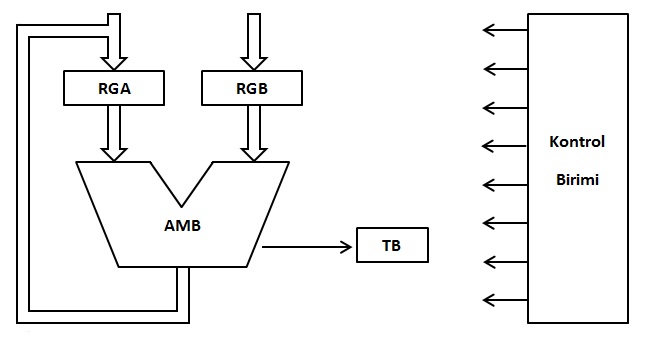
2.5.1.2.1 Sabit Noktalı Sayıların Toplanması ve çıkarılması için gerekli olan donanım

 RGA: RegisterA (AKÜ), RGB: RegisterB, TB: Taşma Bayrağı (Owerflow Flag) 

 A+B işlemi için A sayısının AKÜ’de(RegisterA), B sayısının ise B kaydedicisinde olduğu varsayılır.

Toplama işlemi yapılırken öncelikle kaydedicilerdeki sayıların işaret bitleri kontrol edilir. 

Eğer aküdeki sayının işareti ‘1’ ise bu sayının değili alınır; ‘0’ ise değili alınmadan 3. adıma geçilir. Bu adımda da B kaydedicisindeki sayının işareti kontrol edilir. Eğer B kaydedicisindeki sayının işareti ‘1’ ise bu sayının değili alınarak toplama birimi yardımıyla aküdeki sayı ile toplanır; sonuç aküde kalır.

Eğer B kaydedicisindeki sayının işareti ‘0’ ise bu sayının değili alınmadan 5. adıma geçilir; ve sayı toplama birimi yardımıyla aküdeki sayı ile toplanır; sonuç aküde kalır.

6. adımda ise Taşmanın olup olmadığı kontrol edilir. Taşma yoksa aküdeki sayının yani toplamın işareti yoklanır ve bu işaret ‘1’se aküdeki sayının değili alınarak sonuç bulunur. Taşma varsa TB bayrağı ‘1’lenir ve işlem sonuçlanır; aküde elde edilen  sonuç doğru değildir.

Sabit Noktalı Sayıların Toplanması için akış şeması:

Sabit Noktalı Sayıların Çıkarılması için akış şeması:

Çıkarma işleminin algoritması aşağıdaki şekilde gösterilmektedir. Şekilden de görüldüğü üzere bu işlemin algoritması, toplama işleminin algoritmasından sadece bir fazla adımla farklılaşmaktadır. Bu adım çıkanın (RGB) işaret bitinin değilinin alınması işlemidir: Sign(RGB)=(SignRGB)

Çıkarma işlemi yapılırken öncelikle B kaydedicisindeki sayının işaret bitinin değili alınır. 

Daha sonra aküdeki sayının işareti kontrol edilir. Eğer aküdeki sayının işareti ‘1’ ise bu sayının değili alınır; ‘0’ ise değili alınmadan diğer adıma geçilir. Bu adımda da B kaydedicisindeki sayının işareti kontrol edilir. Eğer B kaydedicisindeki sayının işareti ‘1’ ise bu sayının değili alınarak toplama birimi yardımıyla aküdeki sayı ile toplanır; sonuç aküde kalır.

Eğer B kaydedicisindeki sayının işareti ‘0’ ise bu sayının değili alınmadan, sayı, toplama birimi yardımıyla aküdeki sayı ile toplanır; sonuç aküde kalır.

Sonraki adımda ise Taşmanın olup olmadığı kontrol edilir. Taşma yoksa aküdeki sayının yani toplamın işareti yoklanır ve bu işaret ‘1’se aküdeki sayının değili alınarak sonuç bulunur. Taşma varsa TB bayrağı ‘1’lenir ve işlem sonuçlanır; aküde elde edilen  sonuç doğru değildir.

2.5.1.3 Çarpma işlemi
Çarpma işleminde yöntem, onluk tabanda yapılan çarpma işlemi gibidir; fakat onluk taban yerine ikilik taban kullanılmaktadır. Aşağıdaki örnekte işlem kolaylığı olması açısından tam kısım 2 bit, ondalık kısım ise 3 bit olarak alındı.

Örnek 2.123 1,25 ve 0,875 sayılarının sabit noktalı sayı formatına göre çarpılmasını inceleyiniz.

Sayı_1 = 1.125           →        01.001
Sayı_2 = 0.875           →        00.111

Sayı_1 x Sayı_2 = 0,984375

Sabit noktalı sayı formatı ile elde ettiğimiz sayıyı hesaplarsak:

Sayı = 1 x 2^-1 + 1 x 2^-2 + 1 x 2^-3 + 1 x 2^-4 + 1 x 2^-5 + 1 x 2^-6
Sayı = 0,5 + 0,25 + 0,125 + 0,0625 + 0,03125 + 0,15625 = 0,984375 elde edilir.

2.5.1.3.1 Çarpma işleminin için gerekli olan donanım

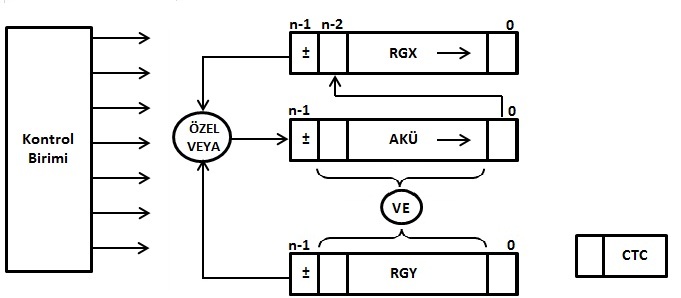
RGX: Çarpanı depolayan kaydedici , RGY: Çarpan2’yi depolayan kaydedici, CTC: Çarpanların bit sayısını depolayan sayaç, AKÜ: Ara sonuç ve sonucun küçük kısmının depolandığı akümülatör.

Çarpma işlemi için gerekli olan donanım:

Çarpma işlemine göre;

Öncelikle X ve Y kaydedicilerine sayılar yerleştirilir; akü ‘0’lanır ve sayaç ayarlanır. Daha sonra X kaydedicisinin en düşük değerlikli bitinin ‘1’e eşit olup olmadığı kontrol edilir. Eğer X kaydedicisinin en düşük değerlikli biti ‘1’e eşitse aküyle Y kaydedicisi toplanır.

Eğer X kaydedicisinin en düşük değerlikli biti ‘0’a eşitse akü ve X kaydedicisi 1 sağa kaydırılır ve akünün en düşük değerlikli biti X kaydedicisinin en büyük değerlikli 2. bitine [(n-2). bit] yerleştirilir.

Sayaç 1 azaltılır. Sayacın ‘0’ olup olmadığı kontrol edilir. Sayaç sıfırlanmışsa işaret biti belirlenir .İşaret biti her iki çarpanın işaret bitlerinin özelveya şemasına verilmesiyle bulunur  ve sonuç aküden elde edilir. Sayaç sıfırlanmamışsa işlemler X kaydedicisinin en düşük değerlikli bitinin ‘1’e eşit olup olmadığının kontrol edildiği yerden devam eder.

Çarpma işleminin algoritması aşağıdaki şekilde görülmektedir:

Çarpma işlemini için akış şeması:

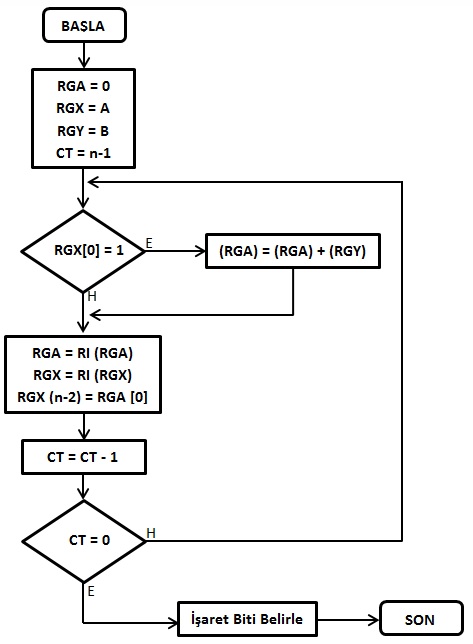
ŞEKİL 2.15 Sabit Noktalı Sayılarda Çarpma İşlemi Blok Diyagramı

2.5.1.4 Bölme işlemi
Bölme işleminde, ilk olarak bölen sayısının en anlamlı biti 1 olacak şekilde sola doğru kaydırma işlemi yapılır. Daha sonra bölünen, bölenden büyük veya eşitse bit değeri 1 olur ve bölen, bölünenden çıkarılarak yeni bölünen değeri elde edilir. Küçük değere sahipse çıkarma işlemi yapılmaz, bölünen aynen kalır ve bit değeri 0 olur. Sonraki aşamada bölen, sağa bir bit kaydırılır. Elde edilen yeni bölen değeri yeni bölünen değerinden çıkarılarak yukarıda belirtilen işlemler tekrar edilir. Örnek olarak çarpma işlemi sonucunda; çarpım sonucunu, çarpanların birine bölerek diğer çarpanı elde edelim.

Örnek 2.124 0,984375 sayısının 0,875 sayısına sabit noktalı sayı formatına göre bölünmesini inceleyiniz.

Sayı_1 = 0,984375 =  000.111111
Sayı_2 = 0,875 = 000.111000 olarak bulunur.

İlk olarak bölen sayımızı en başa 1 gelecek şekilde sola kaydıralım.
Sayı_2 = 11100000 olarak yazılır.

Bölme işleminin sonucunda elde edilen değer 001.001000 şeklinde olmaktadır. Bu sayıyı çevirme işlemi sonucundaki değeri 1.125 olmaktadır. Yani bir önceki işlemimizdeki çarpan değerini elde etmekteyiz.

Q15 FORMATI

Kurallar

    • Sayılar daima 1 ve -1 arasındadır
    • Decimal nokta daima sabit bir noktadadır (örneğin., 0.74, 0.34, vs.)
    • Kesir kısmının başka bir kesir kısmı ile çarpılması bir taşma üretmez (örneğin 0.99 x 0.9999 = 1 den küçüktür)
    • Ardışıl toplamalar taşmaya neden olabilir.
Neden tercih edilir?
    • İşaret işleme çarpma ağırlıklıdır.
    • Fixed-point notasyonu taşmayı önler (Küçük dinamik bölgede faydalıdır).
    • Fixed-point notasyonu ucuzdur.
Sabit-Nokta bir DSP de nasıl gerçeklenir?
    • Sabit-Noktalı DSP lerin çoğunluğu 16 bitliktir.
    • 32767 den -32768 ye kadar sayılar temsil edilebilir.
    • Q15 en çok kullanılan formattır.

Sabit-Noktalı sayıların, bellekte temsili b.c noktalı sayı için tamsayı kısmı aynen alınır, kesirli kısım ise K=kesir*2 biçiminde hesaplanır.

Örnek 4.12 formatında, 3.68 sayısı neye karşılık düşer?
K=0.68 x 4096 =2785 =0xAE1 böylece, sayı 0x3AE1 olacaktır.

Q15 (1.15) formatı için 0.68 sayısı nedir?
K=0.68x32768=0x570A olacaktır

Q15 formatında 0x2218 hangi sayıya denk düşer?
0x2218=8728 sayı=8728/32768 =0.266357

Q15 formatında -0.266357 sayısının bellekteki değeri nasıl olacaktır?
k=(-0.266357)x32768 =(-8728) ikinin tümleyenine çevirelim
65536 – 8728 = 56808 = 0xDDE8

3.68 ile verilen 4.12 formatlı sayının 1.15 formatındaki karşılığı nedir?
4.12 den 1.15’e gidebilmek için noktayı 3 defa sola kaydırmalıyız. Değerin değişmemesi için sayı 8’e bölünmelidir.
3.68/8 =0.46 olacaktır.
 

2.5.2 Kayan Noktalı Sayılar (Floating Point Number)
Kayan noktalı sayılar gerçel sayıların bilgisayar ortamındaki gösterim şekillerinden biridir. Gerçek dünyada sayılar sonsuza kadar giderken, bilgisayar ortamında bilgisayar donanımının getirdiği sınırlamalardan dolayı bütün sayıların gösterilmesi mümkün değildir. Bununla birlikte gerçekte sonsuza kadar giden birtakım değerler bilgisayar ortamında ortamın kapasitesine bağlı olarak yaklaşık değerlerle temsil edilirler. Bu sınırlamaların etkisini en aza indiren, sayıların maksimum miktarda ve gerçeğe en yakın şekilde temsilini sağlayan sisteme "Kayan Noktalı Sayılar" sistemi denir. Kayan noktalı sayılar integer işlemlerden daha yavaştır. Bilgisayar performanslarının karşılaştırılmasında özellikle bilimsel bilgisayarlarda, kayan noktalı sayılar üzerindeki işlem hızı önemlidir. Ölçüm için FLOPS (floating point operation per second) kullanılır. Kayan Noktalı Sayı formatı IEEE-754 tarafından tasarlanmış ve geliştirilmiştir.Aşağıda IEEE/ANSI 754 standardına uygun bir 32-bit kayan noktalı sayı biçimi gösterilmiştir.

e - bias = floor(log₂^sayı)

s:  İşaret bitini temsil etmektedir. İşaret biti sıfıra (0) eşitse sayının pozitif, bire(1) eşitse negatif olduğunu belirtir.

bias:   IEEE 754 standartlarında verilen ve üs sayısından çıkarılan değerdir. 32 bit için bu değer 127 olarak belirtilmiştir.

f:  Burada çarpan olarak verilmektedir. Bu sayı daima sıfır ile bir arasında olmalıdır.
 

Kayan noktalı sayı gösteriminde en anlamlı bit 'işaret biti' olarak tanımlanır, sonra yer alacak bit dizisi 'üs kısmını' ve son kısımdaki bit dizisi de 'ondalık kısmı' ifade etmektedir. Gösterimleri aşağıdaki şekildeki gibidir.

Şekil 2.16 Kayan Noktalı Sayıların Formatı

2.5.2.1 Kayan noktalı sayılar formatı (floating point number format)
Kayan noktalı sayıların temsili için aşağıdaki 3 format belirlenmiştir. Burada sayının işareti (S) her zaman en anlamlı biti temsil eder. Bu bit pozitif sayılar için sıfırı, negatif sayılar için biri ifade eder. e üssü pozitif veya negatif tam sayı olabilir. Kayan noktalı sayıların toplanması ve çıkarılması işlemlerinde üslerin karşılaştırılması gerektiğinden, üslerin işaretlerinin kullanılması gerekmektedir. f ise burada kesir olarak verilmektedir.

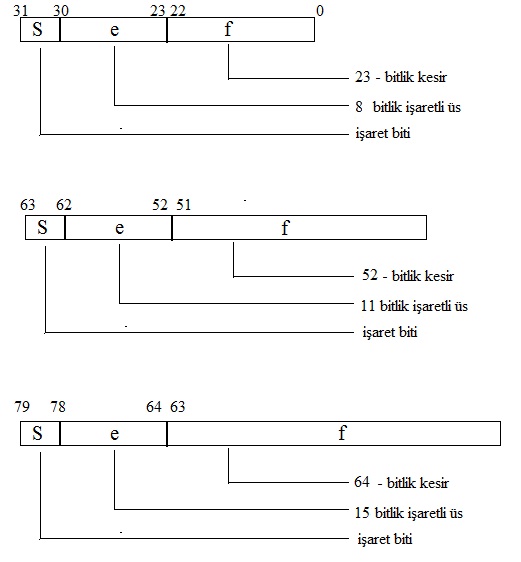
Şekil 2.17 Kayan noktalı Sayılarda 3 Format

Bu formatlar 3 özelliğe sahiptir:

1)  Tek ve çift duyarlı formatlarda mantisinin (sayının kesirli kısmı - f) büyük biti her zaman 1 olduğu için format içinde yer almaz. Fakat sayılar üzerinde işlemler yapıldığında bu bit mantisinin başına getirilir yani, F yerine 1,F kullanılır.

2)  Sayıların temsili ve onlar üzerinde sürdürülen işlemlerde, yalnız binary sayı sistemi kullandığından, formatlarda sayıların taban değeri yani 2 yer almaz.

3) Üslerle ilgili olan işlemlerin kolaylaştırılması amacı ile üssün her zaman artı (+) işaretli gibi görülmesi için üs, yapay bir şekilde artı işaretli sayılar bandına sokulur. Buna göre de formatlarda üssün işareti gösterilmez.

Eğer üs G için m bit ayrılmış ise o zaman üssün alabileceği değer;

– ( 2^m) + 1 ≤ G ≤ (2^m ) – 1 

ifadesiyle belirlenir. Üssün değerine önceden (2m) – 1  ilave edilmiş olursa o zaman söz konusu değer  (2m ) – 1 kadar artırılmış olur ve neticede üssün değeri 0 ile (2(m+1)) –2 arasında değişir gibi görülebilir. Bu şekilde ifade edilmiş olan üssü gerçek üsten ayırabilmek için ona Meyilli üs (Biased Exponent) denir.Böylece meyilli üssün alabileceği değer;

0 ≤ E  ≤ (2^m+1) – 2

ifadesiyle belirlenir. Görüldüğü gibi meyilli üs gerçek üsten 1 bit fazla olan bir yerleşme alanı gerektirir.

Şimdi tek ve çift duyarlı formatlarda mantisinin büyük bitinin yer almaması ve bu formatlarda temsil edilmiş olan mantislerin, işleme sokulmazdan önce başına 1 getirilmesi olayının sebebini açıklayalım:

Tek ve çift duyarlı formatlarda; mantisin değeri her zaman 1 olan büyük bitini format dışına çıkarmakla, mantis için ayrılmış olan n bit bir alanda, (n+1) bit temsil edilebilir. Böylece temsil duyarlılığı 2 kat arttırılmış olur. Örneğin; tek duyarlı formatta mantis için 23 bit bir alan ayrılmıştır. Bu alanın görülen duyarlığı 2^(–23)’tür. Fakat format dışında kalmış olan büyük bitin, bu alandan okunacak olan kodun başına geleceği dikkate alınırsa, söz konusu alanın gerçek duyarlılığının 2^(–24) olduğu anlaşılır.

Söylenilenlere dayanarak tek ve çift duyarlı kayan noktalı formatta temsil edilmiş olan sayının değeri; 

D = (-1)^S  x 1,F x 2^{(E - (2m/ )+ 1)}     formülüyle elde edilir.

Genişletilmiş duyarlı formatta temsil edilmiş sayının değeri ise;

D = (-1)^S x 0,F x 2^{(E - (2m) + 1)}

formülüyle belirlenebilir. Burada S: işaret, F: mantis, E: meyilli üs, m: üs için ayrılmış olan bitlerin sayısını temsil etmektedir.

Örnek 2.125 7 gerçel bir sayısını IEEE 754 standardında kayan noktalı sayı formatına çeviriniz.

 Sayı = 7

7 > 0 olduğu için s = 0 olur.
e - bias = floor(log₂^sayı) = 2
e = 127 + 2 = 129 = (10000001)₂
7 = (-1)₀ . (1 + k) . 2₂
1,75 = 1 + e --> f = 0,75

Ondalık sayıyı ikilik sisteme çevirirken; tam kısmı sürekli ikiye bölüp, kalanları sondan başa doğru yazarız. Böylece; tam sayı kısmını, ikilik sayı sistemde ifade etmiş oluruz. Bu ifadede tam sayı her zaman sıfır olacağından, sadece ondalık kısım ikilik sisteme çevrilecektir. Ondalık kısmın çevrimi aşağıda gösterilmiştir.


Eğer çarpma işlemleri esnasında  sıfır elde ediliyorsa işleme son verilir. Çarpan kısmında IEEE 754 standardına göre 32 bitlik gösterim aşağıda verilmiştir.

Örnek 2.126 45.781₁₀ = 101101.11001₂ sayısı IEEE 32- bit normalize FPN2gösterimi:
Önce sayının en büyük ağırlıklı biti dışında tamamı kesir haline getirilir.
101101.11001₂ = 1.0110111001 x 2⁵
İşaret biti: 0 (pozitif)
Üst (Exs) = 5 +127=132₁₀=10000100₂
Kesir (F) = 0110111001…00(MSB = 1 gösterilmez)

Bunun sonucunda IEEE normalize FPN
FPN₂=01000010001101110010000000000000₂=42B72000h

Örnek 2.127 0.1 için e= -4, f=1.10011001100110011001100₂
Dönüşümden elde edilen bu 32-bit kayan noktalı sonuç yeniden ondalık sayıya dönüştürülürse 0.099999994039536 elde edilir.

2.5.2.2 Toplama ve çıkarma işlemi
Kayan noktalı sayılarda toplama işlemi yapılırken sayıların e ve f değerleri bulunur. Daha sonra eğer normalize işlemi yapılması gerekiyorsa normalize yapılmalıdır. Böylelikle sayılar birbirine uygun şekle dönüştürülerek toplama ve çıkarma işlemleri yapılabilir. Bunları madde halinde inceleyecek olursak;

İlk adım : Toplama işlemini yapabilmek için üsler eşitlenir. Bu işlemde genelde yüksek üsse eşitleme olur.
İkinci adım : Sayılar toplanır.
Üçüncü adım : Sonuç normalize edilir.

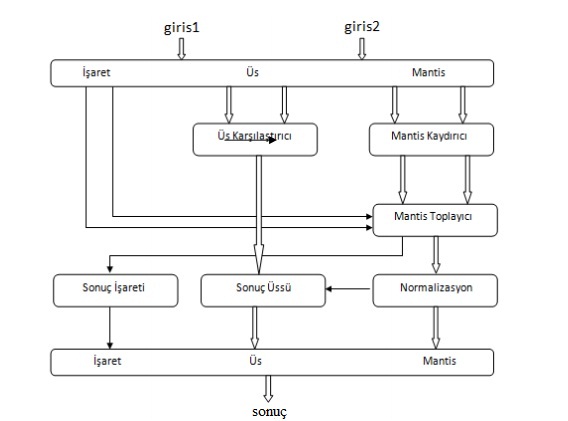Şekil 2.18 Kayan Noktalı Sayılarda Toplama İşlemi Blok Diyagramı

Örnek 2.128 7,362 ve 3,568 sayılarının kayan noktalı sayı formatına göre toplanmasını inceleyiniz.

Sayı_1 = 7,362        Sayı_2 = 3,568

e_1 = 129        1.f_1 = 1,8405
e_2 = 128        1.f_2 = 1,784

Üslü sayılarda toplama işlemi aynı tabanda yapılması gerektiğinden, e_2 ifadesini e_1’e göre normalize edilir;

e_2 = 129        1.f_2 = 0,892

f ifadesi [0 1) aralığında olması gerektiği için; yukarıdaki işlemin soncunda 1.f ifadesini normalize edersek;

e = 130 ve 1.f = 1,36625 olur.

Bu ifadeleri gerçel sayımızı elde etmek için kullanırsak;

Sayı = (-1)0(1,36625)23
Sayı = 1,36625 x 8 = 10,93 elde edilir

Gerçel sayılarımızın toplamı da 7,362 + 3,568 = 10,93 elde edilir.
Çıkarma işlemi de toplam işleminde olduğu gibi yapılmaktadır.

2.5.2.3 Çarpma işlemi
Kayan noktalı sayılarda çarpma işlemi toplama ve çıkarma işlemlerinde olduğu gibi e ve f değerlerinin bulunmasıyla başlar. Daha sonra e ve f değerleri kendi aralarında çarpılırlar. Normalize ve işlemi gerekiyorsa yapılır. Geriye gerçel sayıları elde etmek kalır. O da elde edilince çarpma işlemi kurallarına uygun bir şekilde gerçekleştirilebilir. Bunları madde halinde sıralayacak olursak;

İlk adım : Üsler toplanır.
İkinci adım : Katsayılar çarpılır.
Üçüncü adım : Sayıların işaretleri birbirine eşitse bulduğumuz sonucun işareti pozitif olur; eşit değilse negatif olur.
Dördüncü adım : Sonuç normalize edilir.

Şekil 2.19 Kayan Noktalı Sayılarda Çarpma İşlemi Blok Diyagramı

Örnek 2.129 7,362 ve 3,568 sayılarının kayan noktalı sayı formatına göre çarpılmasını inceleyeniz.

Sayı_1 = 7,362     Sayı_2 = 3,568

e_1 = 129        1.f_1 = 1,8405
e_2 = 128        1.f_2 = 1,784

f ifadesi [0 1) aralığında olması gerektiği için; yukarıdaki işlemin soncunda 1.f ifadesini normalize edersek;

e = 131  1.f =1,641726 olarak bulunur.

Bu ifadeleri gerçel sayımızı elde etmek için kullanırsak;

Sayı = (-1)⁰ (1,641726)2⁴
Sayı = 1,641726 x 16 = 26,267616 elde edilir.

Gerçel sayılarımızın çarpımı da 7,362 x 3,568 = 26,267616 elde edilir.

2.5.2.4 Bölme işlemi
Kayan noktalı sayılarda bölme işleminde yine e ve f değerleri bulunur. Bulunan e ve f değerlerinden sonra gerçel sayılar elde edilerek bölme işlemi gerçekleştirilebilir.

Örnek 2.130 7,362 sayısının 3,568 sayısına kayan noktalı sayı formatında bölünmesini inceleyiniz.

Sayı_1 = 7,362        Sayı_2 = 3,568

e_1 = 129        1.f_1 = 1,8405
e_2 = 128        1.f_2 = 1,784

Bu ifadeleri gerçel sayımızı elde etmek için kullanırsak;

Sayı = (-1)⁰ (1,031670404)2¹
Sayı = 1,031670404 x 2 = 2,063340807 elde edilir.

Gerçel sayılarımızın bölümü de 7,362 / 3,568 = 2, 063340807  elde edilir.

2.5.2.5 Kayan noktalı sayılarda karmaşıklıklar

Sayıları kayan noktalı şekilde ifade etmek çeşitli karmaşıklıklara yol açabilir.

• İşlemlerin daha karmaşık olması
• Toplama ve çıkarma işlemlerinde aritmetik taşmanın yanında, duyarlılıktan taşma olasılığının olması
• Standardın korunmasının zor olması
• Çok küçük sayıların olağanlaştırılmış biçimde gösterilmesinin mümkün olmaması
• Yuvarlama, işlemlerin 'sonsuz veya sayı değil' sonuçlarıyla karşılaşma

bu karmaşıklıklardan bazılarıdır. IEEE 754 standardına göre sonsuz, sayı değil gibi kavramlar ve yuvarlama işlemi için de çeşitli metotlar geliştirilmiştir.

2.5.2.6 Aritmetik hata hassasiyeti

Sabit yada kayan noktalı işlemlerde farklı hassasiyetler söz konusudur.
    •Taşma olmaması için gerekli bit uzunluğu farklı olacaktır
    •Sabit noktalı aritmetikte toplama ve çıkarma kuralları kesindir.
    •Toplamada tasma
    •Çıkarmada alt taşma bayrağı
    •Çarpma gerekli kelime uzunluğu
    •Kayan noktada kelime büyümesi farklıdır.
    •Kelime büyümesi çok fazla olmaz.
    •Tek hassasiyetli hesaplamalarda mantis için daima bir yuvarlatma gürültüsü vardır (Çift uzunluklu çarpım sonucu, tek uzunluğa sıkıştırılmıştır).
    •Kayan noktada mutlak hatalar daha hızlı artar.